This is what I’ve learned from the workshop by David P. Sanders

We will simulate the dynamics of an epidemic, i.e, an outbreak of an infectious disease. In a population of people with N individuals we will be interested in how the number of susceptible (S), infectious (I) and recovered (R) individual changes over time. We will begin by looking at simple models that take into account only total numbers of people, by the end of the workshop we should be able to structure a more complicated individual - based or agent - based simulation, where we model individual people moving around space and interacting with one another.

For Simplicity, those individuals will be modelled as random walks on a grid, i.e, points that choose a neighbouring grid point at random to jump to.

Table of Contents

• Generic programming
• Composite types
• (Outer) constructors
• Generic programming with Types
• Types for agents
• Composition and Parametrised Types
• Spatial SIR model
• Dynamics

Generic programming: Random walks

Each step roughly corresponds to a different function. Each different type of walker will need a different way to:

• initialize() itself and then
• move() which will return the new position chosen by the walker.

Therefore a walk of length T is given by the following function

function walk(T)
    pos = initialize()
    trajectory = [pos]    # make a Vector that contains just the current value of `pos`
    for t in 1:T
        new_pos = move(pos)
        push!(trajectory, new_pos)   # append to the Vector
        pos = new_pos     # update for next iteration
    end
    return trajectory
end

We noticed that this depends on the functions initialize() and move() that should be defined on the global scope. Since a random walk can be in n dimension, we would like to be able to run the same function of all dimension, this is what is called generic programming.

function walk(initialize, move, T)
    pos = initialize()
    trajectory = [pos]
    for t in 1:T
        pos = move(pos)               # *update* the value pointed to by `pos`
        push!(trajectory, deepcopy(pos))  # at the cost of needing to copy `pos` when we store it if it is a vector
    end
    return trajectory
end

This way we can have different initialize() and move() functions depending on the dimension of the walker and we will be able to recover the trajectory calling the same walk function.

Now the question is, how can we efficiently store information about each walker? we would like to now not only the trajectory but also if he is susceptible, infected or recovered. This leads us to the following section.

Composite types

The main idea is to collect up or aggregate all relevant information into a new data structure, called a composite type (or custom type, aggregate type, user-defined type, …).

Basically we want to be able to specify the “template” / “shape” / “structure” for a bag or box that will contain all the relevant information; this specification is the type itself. Then we need to produce objects which have that structure, i.e. which contain the corresponding variables; these are called instances.

In Julia this is accomplished using the struct keyword (short for “structure”). For example, we can make an object that contains the $x$ and $y$ coordinates of a walker in 2 dimensions as:

struct Walker2D
    x::Int64
    y::Int64
end

(Outer) constructors

Suppose we want walkers to be born at the origin unless otherwise stated. We don’t want to have to write Walker2D(0, 0) each time; we would like to just write Walker2D(). In other words, we want to add a new method to the function Walker2D:

Walker2D() = Walker2D(0, 0)

Such a constructor is called an outer constructor, since it lives outside the definition of the type.

Making walkers move

We are not allowed to modify the fields of a walker because we defined the structure as being immutable (if we want it to be mutable we need to specify it). Usually this will give us better performance. So in order to make our walker move, we need to create a new object with the new position. This could seem expensive, but in fact the Julia compiler will often be able to completely remove this object creation and produce code that is just as efficient as if there were no object at all!

Suppose we want to only move on the $ x - axis $ then we can just define:

move(w::Walker2D) = Walker2D(w.x + rand( (-1,1) ), w.y)

Now supposed we need to defined a function that moves us to an adjacent point at random, then we can just throw a coin an choose a direction based on that result.

function jump(w::Walker2D)
    r = rand()
    if r > 0.5
        return Walker2D(w.x + rand( (-1,1) ), w.y)
    else
        return Walker2D(w.x, w.y + rand( (-1,1) ) )
    end
end

Generic programming with Types

Before we create a walk function that depends on the functions initialize() and move(), but what if we just have one of each function with different methods? this solution should be better, otherwise we would have to define functions initialize_1D() and initialize_2D() to pass it as an argument an make a distinction between 1 dimension and 2 dimension walkers.

"Calculate the trajectory of a walker `w` for time `T`."
function walk(w, T)
    trajectory = [w]   # store the current (initial) position of `w`
    for t in 1:T
        w = move(w)    # update the value bound to `w`
        push!(trajectory, deepcopy(w))   # store the current value
    end

    return trajectory
end

We have not specified a type of $w$ this means that if we have a move function that works for instance for Integer numbers (BigInt, Int64 and so on) it should work and it should also work if we have a Walker2D as an argument.

Types for agents

We are getting towards our goal of putting everything together to make a model of people moving around and interacting with one another. Most people start off susceptible, but when an infectious person meets a susceptible the infection is transmitted with a certain probability.

We will make an individual-based model, also called an agent-based model. We need a struct called Agent that contains whatever information an agent needs. In our case we will need a position and an infection status.

The position will behave almost like a normal random walk that we have seen before, while the infection status needs to reflect whether the agent is susceptible (S), infectious (I) or recovered / removed (R).

Enums

We could represent the infection status simply using an integer, e.g. 0, 1 or 2. But then our code will be hard to read, since we will be comparing the infection status to numbers all the time without remembering which one is which.

A nice solution is just to use @enums macro.

@enum InfectionStatus S=1 I R   # specify that `S` corresponds to the value 1

We will have a new Type InfectionStatus, with possible values S, I and R that also store a numerical value $ S = 1 $, $ I = 2$ and $ R = 3$. Then we can do Int(I) and it will return the integer 2, we can also do

status = I
if status == I
    println("infected!")
end

and get infected! as a result. This way the InfectionStatus information gets easy to manipulate and remember in our code.

Composition and Parametrised Types

We can place one object inside another one.

Suppose we have defined a SimpleWalker2D structure as follows.

struct SimpleWalker2D
    x::Int64
    y::Int64
end

Then we can define an Agent as:

struct Agent
    position::SimpleWalker2D
    status::InfectionStatus
end

Then we can create an infected Agent in position $(1,2)$ by simply doing w = SimpleWalker2D(1,2) and then a = Agent(w,I).

As we learned before, we would like to have our program a bit more generic. One way of doing it is by parametrizing Types:

struct Agent{T}
    position::T
    status::InfectionStatus
end

Sometimes beeing too generic can cause troubles if not careful. Then we can parametrise for only some Types. Suppose there is a common abstract type AbstractWalker for all of the possible types that we want to be able to use for T (this can be 1,2 and 3 dimension walkers for example), then we can write:

struct Agent{T <: AbstractWalker}
    position::T
    status::InfectionStatus
end

Spatial SIR model

Now we are ready to build the spatial model. It will consist of walkers moving in a 2D box. This was an exercise left to the audience at the end of the talk, so we will solve it as it is written on the notebook.

Confinement inside a box

We need agents to live inside a box so that they don’t disperse.

Exercise

• Make a ConfinedWalker2D type. Its fields are a Walker2D object and a box size, L.

struct Walker2D
   x::Int64
   y::Int64
end

struct ConfinedWalker2D
    w::Walker2D
    L::Int64
end

The important part here is that we just give the size of the box as a parameter. We do not do an inner constructor that checks if the position of the walker is inside the box. This is because inner constructors can be bothersome so we just need to keep in mind that we should check boundaries at some future function.

• Extend move to ConfinedWalker2D. If the walker tries to jump outside the box, i.e. outside the sites 1 to 𝐿 , in either direction, then it remains where it is.

function move(cw::ConfinedWalker2D)
    r = rand()
    step= rand([-1,1])
    if r > 0.5
        posx = cw.w.x + step
        posy = cw.w.y
    else
         posx = cw.w.x
         posy = cw.w.y + step
     end
    if (posx <= cw.L)&& (1 <= posx)&&(posy <= cw.L)&& (1 <= posy)
        w = Walker2D(posx,posy)
        return ConfinedWalker2D(w, cw.L)
    else
        return cw
    end
end

• Make a confined Agent and calculate and draw its trajectory to make sure it stays inside the box.

struct Agent{T}
    cw::T
    status::InfectionStatus
end

Let’s consider $L = 6$ and initial position $(5,5)$

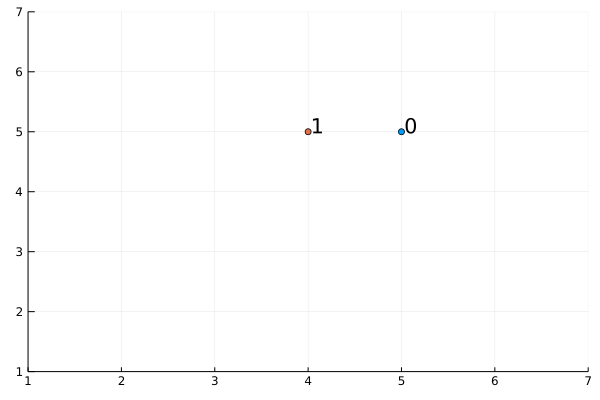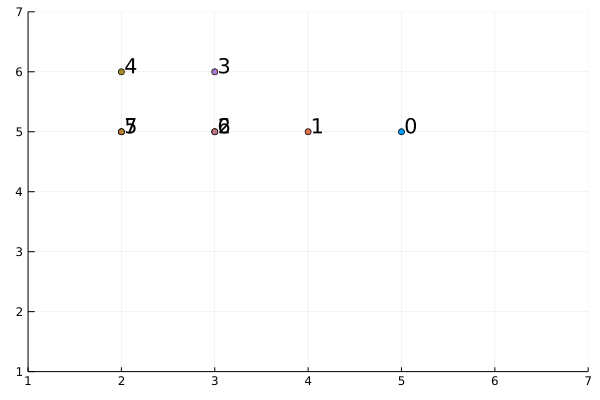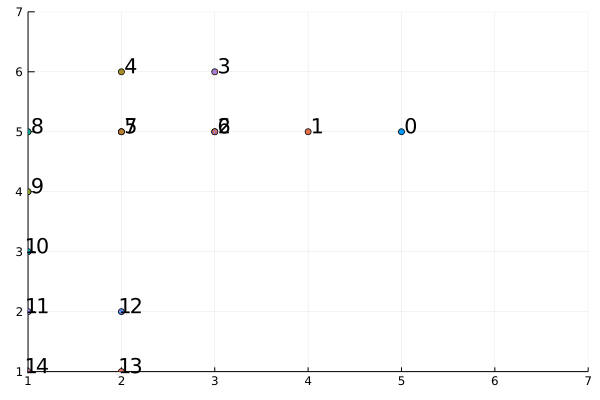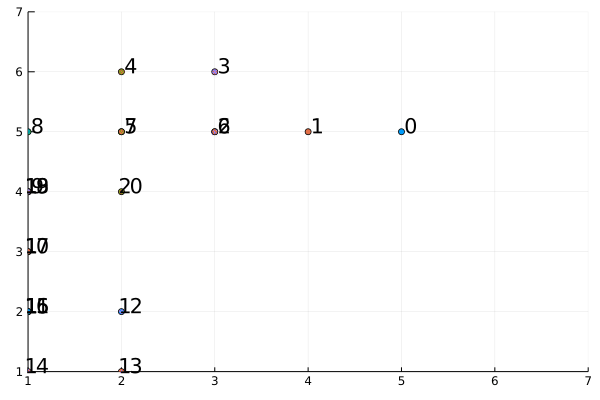
We can see how it does not move outside the border and stays in the same position in the $16th$ move for example.

Initialization

Exercises

• Write a function initialize that takes parameters 𝐿, the box length, and 𝑁, the number of agents. It builds, one by one, a Vector of agents, by proposing a position for each one and checking if that position is already occupied. If it is occupied, it should generate another one, and so on until it finds a free spot. All of the agents should have state S, except for one infectious individual (I).

To do this you should write a function check_occupied that checks if a particular position is occupied.

function check_ocupied(w::Walker2D,v)
    m = length(v)
    if m == 0
        return false
    else
        for i = 1:m
            if (w.x == v[i].cw.w.x) && (w.y == v[i].cw.w.x)
                return true
            end
        end
        return false
    end
end

function initialize(L,N)
    i= 0
    v = []
    while i < N
    x = rand(-L:L)
    y = rand(-L:L)
    w = Walker2D(x,y)
        if !check_ocupied(w,v)
            a = Agent( ConfinedWalker2D(w,L), S)
            push!(v,deepcopy(a))
            i = i+1
        end
    end
    index = rand(1:N)
    v[index] = Agent(v[index].position,I)
    return v
end

• Write a function visualize_agents that takes in a collection of agents as argument. It should plot a point for each agent, coloured according to its status

function visualize_agents(v)
    m = length(v)
    x = SA[zeros(m)]
    y = SA[zeros(m)]
    infection_status = []
    for i = 1:m
        x[1][i] = v[i].cw.w.x
        y[1][i] = v[i].cw.w.y
        push!(infection_status,deepcopy(Int(v[i].status)))
    end
    return scatter((x,y) , c = infection_status, ratio =1, leg = false)
end

• Run these functions to visualize the initial condition.

Let’s consider $L = 6$ and $N = 20$. Then we get the following:

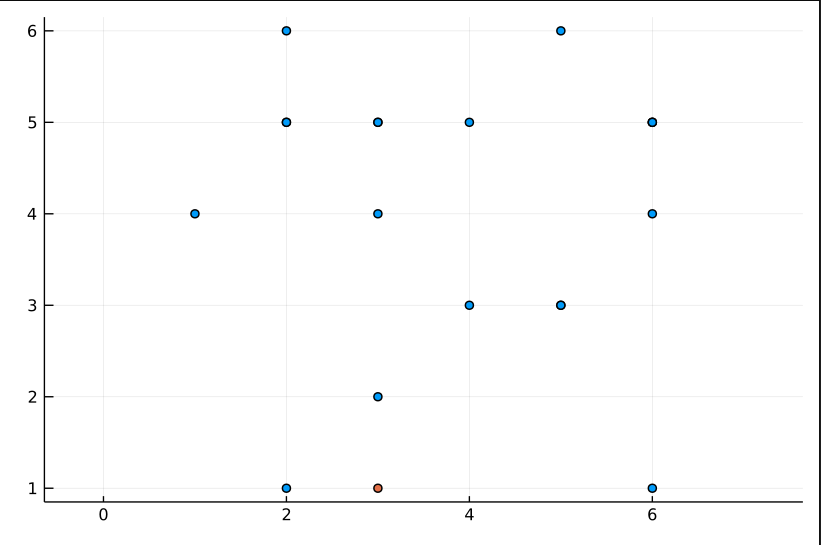
Dynamics

Now we just need to simulate the dynamics of the system. We will consider parameters $p_l$ and $p_R$, the probabilities of infection and recovery at each time step, respectively. The system evolves as follows:

• First the system is initialized with only one random infected agent.
• Secondly, a single agent choosen randomly, call it $i$ tries to move to an adjancent position. If the position is ocuppied, by agent $j$, then neither of them move, but they interact as follows:
• If agent $i$ is infected and agent $j$ is susceptible then agent $j$ gets infected with probability $p_I$
• If agent $i$ is infected, it recovers with probability $p_R$.

We do this part defining step() function

Notice that this model does not allow a recovered agent to get infected again.

Then the step! function looks as follows:

"Receives a vector of agents and the required probabilities,
returns a modified agent vector"
function step!(v, pI, pR)
    n = length(v)
    i = rand(1:n)
    cwi = move(v[i].cw) # we move agent i 
    index = check_ocupied2(cwi.w,v) # Give us [] or the index j of agent
    m = length(index) # can be 0 or 1
    if m == 0
        v[i] = Agent(cwi, v[i].status)
    else
        for j in index
            v[i],v[j] = infection(v[i],v[j], pI, pR)
        end
    end
    return v
end

Infection() function makes the interaction between the agents $i$ and $j$ following the previous rules.

Let’s see how the system evolves after $1000$ steps. For this we will use $L = 6$ , $N = 30$, $p_I = 0.5$ and $p_R = 0.05$. Orange means infected, Blue is susceptible and Green is recovered.

Final thoughts

This workshop and to be honest most of JuliaCon 2020 workshops were amazing, as you can learn so much. There is a known saying about Mathematicians being able to code and solve problems at the cost of doing a really long, slow and bad algorithm. Going to this workshops and trying to learn as much Julia as possible during JuliaCon is making me improve a lot in terms of coding and knowing the capabilities of the language, so I recomend checking the workshops videos on youtube